|
|
Pulser
a neologism, is
an acronym that
combines the words "pulse" and "series."
Pulser refers to
a sequence of two terms that define all ellipses and many sequences and series.
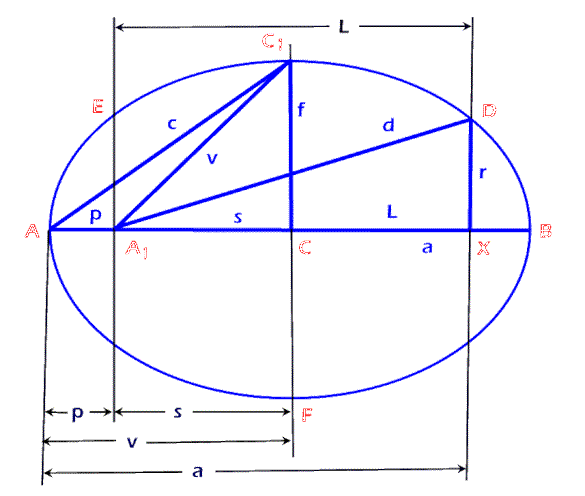
For an ellipse, the value of a Pulser's first term defines
the perigee, "p," which is the distance from an end of the major diameter to the
nearest focus; the value of a Pulser's second term defines the soliton, "s,"
which is the distance from the midpoint of the major diameter to either focus;
the value of the vector, "v," is the distance from the midpoint of the major
diameter to either end of the major diameter, which is always equal to the sum of the
Pulser's two terms; (the vector, "v," is also the distance from either focus to the
end of the minor diameter); the value of the focal length, "l," for
any ellipse, is twice the
second term of the Pulser.
v = p + s
l = 2s
The Pulser is the first two terms of an
additive series
or sequence if those terms define the entire series or sequence.
An examples of such are:
The Brunardot Series: x, x2-x, x2, 2x2-x,
3x2-x, ...; where the Pulser is x and x2-x.
The Fibonacci sequence: 1, 1, 2, 3, 5, 8, 13, ...; where the Pulser is 1
and 1.
The Revised Fibonacci sequence: 1, 0, 1, 1, 2, 3, 5, 8, 13, ...; where
the Pulser is 1 and 0.
The Golden Sequence: Phi, 1, Phi2, Phi2+1, 2Phi2+1, 3Phi2+2, 5Phi2+3, 8Phi2+5, 13Phi2+8, ...;
where the Pulser is Phi and 1.
For sequences and series, the terms of a Pulser are,
respectively, the first and second term of said sequences and series when these
two terms and their relationship are all that is needed to define said
sequences and series.
The characteristics of an ellipse, and/or its derivative sequences and series, are
determined by its Pulser.
An ellipse is a Brunardot ellipse when the second term of a Pulser is the
Natural function, "x2 - x," when the first term is "x."
A Brunardot ellipse is a Conceptual ellipse when the first term of its Pulser is
an integer.
A Brunardot ellipse is a Golden ellipse when the second term of its Pulser has
the value of the Conceptual Unit, "1" and the value of the first term is the Golden Ratio, "Phi."
A Conceptual ellipse is a Pulsoidal ellipse when the radius, r," is the square of
the first term of the Pulser (perigee, "p"). Every Pulsoidal ellipse consists of unending harmonic
iterations.
|
|