 |
| Riemann was one
of the finest pure mathematicians of his century. ...within his mind
burned the desire to understand the nature of the physical
world... Anticipating relativity and modern cosmology, Riemann understood that in order to grasp the meaning of the physical world, one had to develop a deep understanding of...geometry. Amir D. Aczel [circa 1953- ] -God's Equation, 1999 |
The general theory of relativity splendidly
justified his (Riemann's) work. In the mathematical apparatus developed from Riemann's address, Einstein found the frame to fit his physical ideas, his cosmology, and cosmogony: and the spirit of Riemann's address was just what physics needed: the metric structure determined by data. Hans Freudenthal [1905-1990] -Dictionary of Scientific Biography, 1970-90 |
| I've often wondered
how Einstein could...make such a simple
assumption... the universe is so
simple that we can analyze it in a one-dimensional differential equation--everything a function of time...Einstein...was awfully close to the
truth--that's the way the universe looks. James Peebles [1935- ] -Origins: The Lives and Worlds of Modern Cosmologists, 1990, by A. Lightman and R. Brawer |
Researchers have
hypothesized that Einstein extended his quest to the entire universe
because of an idea of Ernst Mach. ...Mach's law of inertia. ...says that...inertia...is an effect...due to...all other mass in the universe. Amir D. Aczel [circa 1953- ] -God's Equation, 1999; and Max Born [1882-1970] -Einstein's Theory of Relativity, 1965 |
|
|
||||
|
Unimetric Structural Parts |
|
|
|
|
Sequences of the Brunardot Series |
||
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
... |
Infinity |
|
1 |
0 |
1 |
1 |
2 |
3 |
5 |
8 |
13 |
21 |
34 |
... |
Reality |
|
2 |
2 |
4 |
6 |
10 |
16 |
26 |
42 |
68 |
110 |
178 |
... |
Universe |
|
3 |
6 |
9 |
15 |
24 |
39 |
63 |
102 |
165 |
267 |
432 |
... |
" " |
|
4 |
12 |
16 |
28 |
44 |
72 |
116 |
188 |
304 |
492 |
796 |
... |
" " |
|
5 |
20 |
25 |
45 |
70 |
115 |
185 |
300 |
485 |
785 |
1270 |
... |
" " |
|
6 |
30 |
36 |
66 |
102 |
168 |
270 |
438 |
708 |
1146 |
1854 |
... |
" " |
|
7 |
42 |
49 |
91 |
140 |
231 |
371 |
602 |
973 |
1575 |
2548 |
... |
" " |
|
8 |
56 |
64 |
120 |
184 |
304 |
488 |
792 |
1280 |
2072 |
3352 |
... |
" " |
|
... |
... |
... |
... |
... |
... |
... |
... |
... |
... |
... |
... |
... |
|
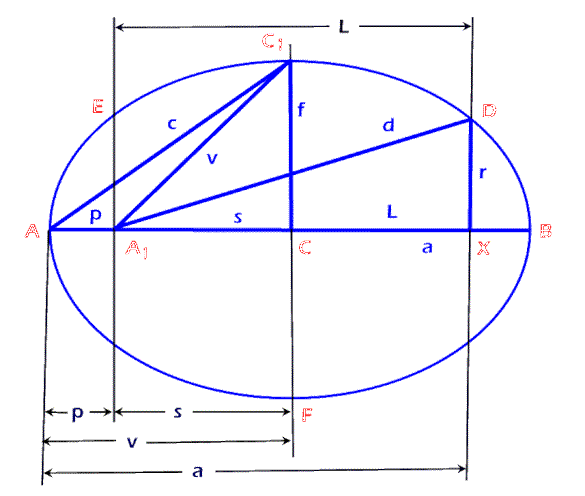
The Golden Sequence is an interesting sequence in the manner of a Brunardot Series Sequence beginning with Phi, F. Note that the coefficients, of Phi, F, in the second form of the Golden Sequence, match the "completed" or "revised" Fibonacci series, which generates the sphere of Reality. |
||
|
F |
1 |
F2 |
F2 |
2F2 |
3F2 |
5F2 |
8F2 |
13F2 |
21F2 |
34F2 |
Golden Sequence |
|
|
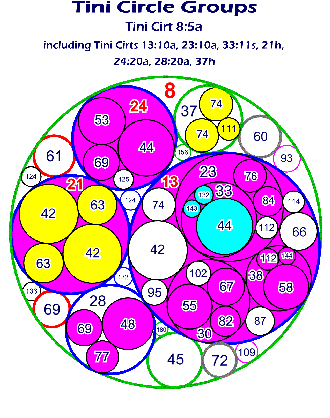
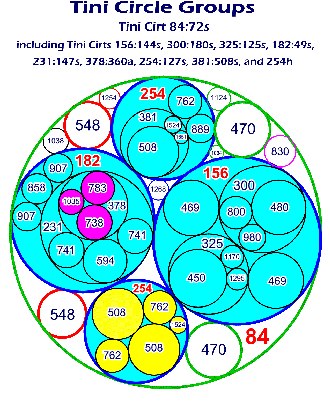
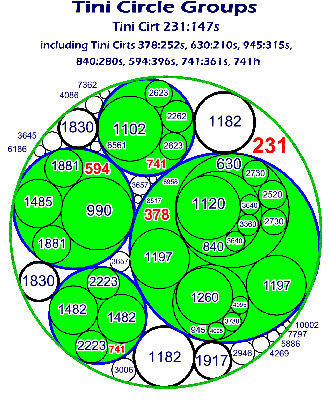
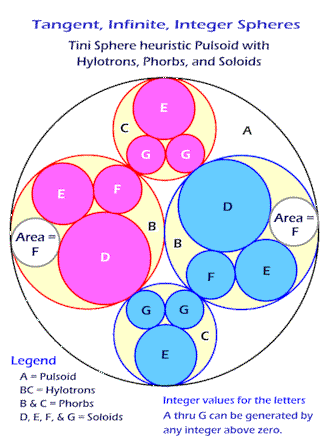
| A Tini Circle
Group contains circles wherein every
circle is tangent to its adjacent circles; and, every curvature (the reciprocal of a circle's
radius,
1/r) is an integer. There is a circle, with a decreasing integer radius, that is tangent to all adjacent circles that continues to the infinitesimal, for every open space between every tangent circle, and within, every tangent circle; that is: |
| Within
any group of three mutually tangent integer circles that are within any
circle, there exists no space, to the infinitesimal, that
does not contain an integer radius circle that is tangent to
all of its adjacent group of three mutually tangent circles. The formula, for four mutually tangent circles (where a, b, c, and d represent the circles' curvature), is: |
||
|
a2 + b2 + c2 + d2 = (a + b + c + d)2 / 2 |
||
The curvature is negative or positive depending upon whether the curvature is concave or convex. |
Every integer radius belongs to an array that contains endless sequences and terms; each array is defined by two, and occasionally only one, integer; these defining integers are referred to as: Tini Cirts. Tini Cirts are an acronym for Tangent, Infinite, Integer, Circle Terms. There are at least three Tini Cirts that begin with the integer One, 1, for every other Natural Integer, above Zero, there are more Tini Cirts. |
 |
 |
||
 |
 |
||
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
There is one Universe.
It is perpetual, in equilibrium;
and, a manifestation of the
Unified Concept; thus;
. . . the Fundamental Postulate.
also,
are a single discipline, Philogic,
which proclaims perpetuity
and the nexus of Life; such is
. . . Conceptualism.
This symbol indicates:
not complete, or more information needed . . .
please E-mail
your information, corrections, documents, photos,
inquiries, or any other needs to:
Brunardot@Brunardot.com
Return to Top of Page
Brunardot.com website
Dedicated to Giordano Bruno, Leonardo da Vinci.
Leonardo da Pisa, Arturo Meniot, & Denis Diderot
Terms of: © Copyright 1999-2017 by Brunardot
CONCEPTUAL Applications
Family of Informational Websites
Emphasizing Philogic, a discipline that overarches
Science, Theology, and Philosophy (STP)Website Design by: CONCEPTUAL Applications
a division of: WebComm21